一句话总结

Falcon LLM 团队提出可学习的逐行和逐列乘数，可在训练过程中动态缩放权重矩阵，克服权重衰减与随机梯度噪声引起的次优平衡；该自适应方法优于调优的 μP 乘数，且性能媲美从 Adam 切换到 Muon 的提升，在降低调参开销的同时，为对称性和宽度缩放提供了实用洞见。

主要贡献

• 大型语言模型预训练中的权重衰减（WD）会引发噪声-WD 平衡，导致权重范数与学习率和 WD 超参数成比例缩放，限制了模型根据数据自适应调整最优尺度的能力。本文识别出该平衡范数为次优伪影，并提出可学习乘数以突破此限制。

• 该方法引入可学习的标量、逐行和逐列乘数，对权重矩阵进行重参数化，使模型能够学习数据自适应的尺度，在残差块间实现更丰富、更多样化的表示，优于经过良好调优的 $\mu$μP 基线，同时显著降低调参开销。

• 在标准与混合注意力-SSM 架构上，对 Adam 和 Muon 优化器均进行了验证，可学习乘数一致提升下游性能，达到切换优化器的增益水平，同时引发关于对称性和宽度缩放的实际思考。

引言

作者研究了权重衰减（WD）在大型语言模型（LLM）训练中的作用，WD 广泛应用于 AdamW 和 Muon 等优化器中，以稳定训练并提升性能。从随机梯度噪声的角度看，WD 与噪声引起的权重增长保持平衡，导致权重范数出现可预测的平衡状态，其缩放与学习率和 WD 超参数相关。然而，这种平衡限制了模型权重从数据中学习最优尺度的能力，实质上制约了表征能力。为解决此问题，作者提出可学习乘数（LRM），一种重参数化技术，通过在矩阵层上引入可学习的标量或向量因子，将权重尺度与优化超参数解耦。这使得权重在训练过程中可自由调整其尺度，从而摆脱噪声-WD 平衡。实验表明，LRM 能在残差块间实现更丰富、更多样化的特征表示，并在长周期预训练中持续优于基线。该方法在多种架构（包括混合注意力-SSM 模型）和优化器（如 Adam 和 Muon）上均表现稳健，展现出广泛适用性。

方法

作者采用重参数化方法，应对大型语言模型训练中随机梯度噪声与权重衰减相互作用所导致的次优权重范数平衡。该平衡限制了权重矩阵的尺度，使其难以适应数据特定的表示。为克服此问题，该方法引入可学习乘数，使模型能够动态调整其内部表示的尺度。核心思想是通过引入可学习参数，将权重矩阵的尺度与噪声-WD 平衡解耦，使其能自由适应数据分布。

该框架从标量乘数重参数化开始，有效权重矩阵 $\overline{W}_{ij}$Wij​ 表示为 $\overline{W}_{ij} = s W_{ij}$Wij​=sWij​，其中 $s \in \mathbb{R}$s∈R 为可学习标量。这使得权重矩阵的整体范数可独立于噪声-WD 平衡进行调整，否则 $\|W\|$∥W∥ 将被约束为与 $\sqrt{\eta / \lambda}$η/λ​ 成比例的固定值。标量乘数 $s$s 学习对矩阵 $W_{ij}$Wij​ 进行缩放，使完整矩阵范数 $\|\overline{W}\| = s \|W\|$∥W∥=s∥W∥ 能够最优地适应数据。该重参数化应用于模型中的线性层，使模型能够摆脱次优平衡范数。

在此基础上，作者将方法扩展至向量乘数，引入逐行和逐列缩放参数，进一步细化尺度适应。重参数化变为 $\overline{W}_{ij} = r_i W_{ij} c_j$Wij​=ri​Wij​cj​，其中 $r_i \in \mathbb{R}^{d_{\text{out}}}$ri​∈Rdout​ 和 $c_j \in \mathbb{R}^{d_{\text{in}}}$cj​∈Rdin​ 为可学习向量。这允许权重矩阵的各个行和列范数独立缩放，解决了“即使单行和单列的范数也受噪声-WD 平衡约束”的假设。通过链式法则推导出重参数化矩阵 $W_{ij}$Wij​ 以及乘数 $r_i$ri​、$c_j$cj​ 的梯度，结果表明行和列乘数在其各自维度上累积梯度，从而降低梯度噪声，并防止因布朗运动扩张而必须依赖权重衰减的情况。

该方法设计为与标准训练框架兼容。推理时，可学习乘数可与对应权重矩阵合并为有效矩阵 $\overline{W}_{ij}$Wij​，消除任何内存或延迟开销。训练时考虑两种实现策略：一种在前向传播中显式使用重参数化表达式，依赖自动微分；另一种在前向和反向传播中使用有效矩阵，而将乘数动态更新交由优化器层面手动处理。后一种方法可减少因额外参数带来的吞吐量下降。

作者还解决了多个可学习因子在乘积中引发的对称性不稳定性问题。此类对称性（如乘法对称性和归一化对称性）可能导致某些参数范数无界增长而不影响模型输出，引发数值不稳定。为缓解此问题，对乘数施加微小权重衰减，可在不显著影响性能的前提下稳定训练。

实验

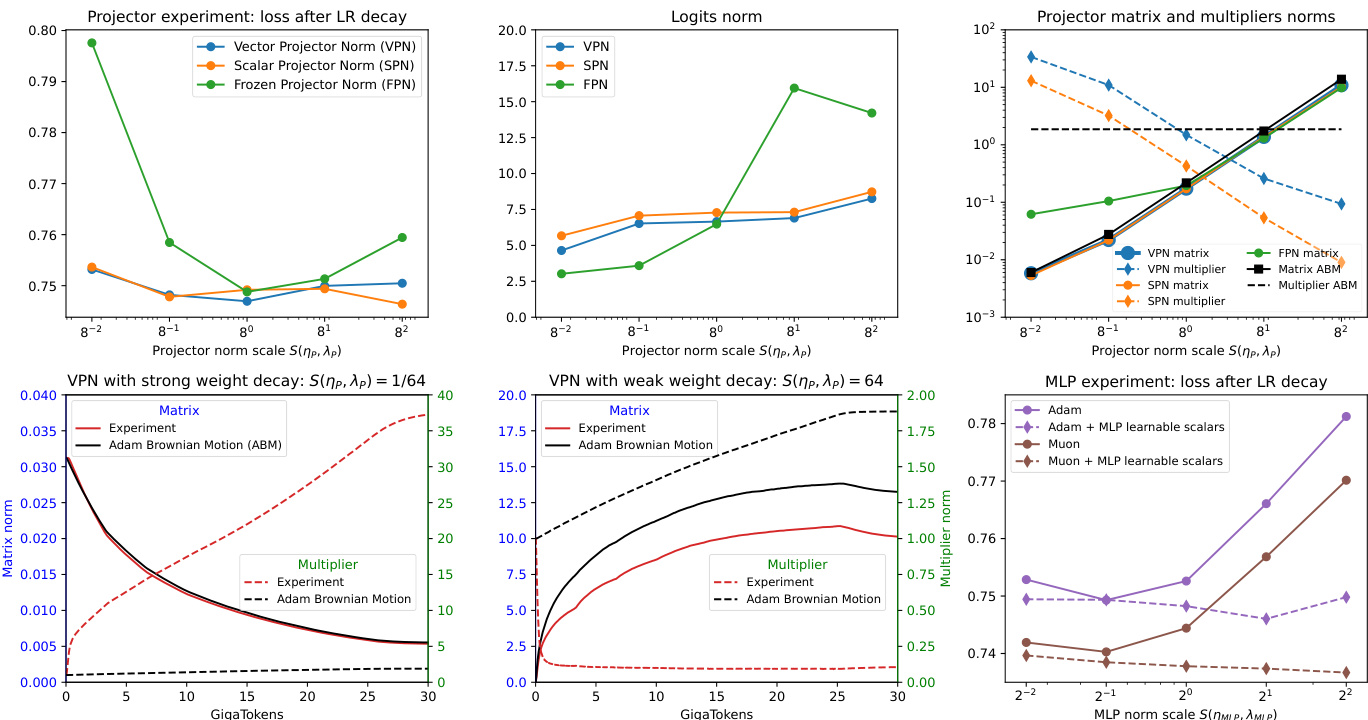
• 投影器与 MLP 实验验证了矩阵层陷入噪声-WD 平衡，而可学习乘数（标量/向量）可实现尺度自适应，在极端尺度缩放下仍保持稳定的 logits 和残差范数。在 LM 头和 MLP 块上，固定投影器范数的配置在极端尺度下性能下降，而配备乘数的版本则保持稳定性能和 logits 范数。
• 乘数实验表明，可学习乘数能独立于噪声-WD 平衡调整其尺度，ABM 模拟结果证实乘数轨迹与噪声驱动动力学相分离，确认乘数不受平衡缩放约束。
• 深度与宽度尺度分析显示，标量乘数可实现模型深度上残差输出范数的递增，并促进注意力与 MLP 层的特征尺度多样性，注意力与 SSM dt 投影表现出层间特定的尺度专长。
• 宽度缩放实验表明，矩阵范数在模型宽度变化时保持恒定，打破了仅依赖学习率的 μP 缩放规则。可学习乘数能自动适应宽度，实现稳定的激活范数（投影器、SSM dt、注意力 QK），并近似按预测缩放（d⁻¹, d⁻²），表明其具备有效自动适应能力。
• 梯度裁剪实验显示，将乘数梯度纳入范数计算会导致过度裁剪和性能下降；排除乘数梯度可恢复稳定性并提升训练效果，凸显可学习乘数需谨慎集成。
• 乘数调参消融实验表明，可学习乘数始终优于非可学习配置，最佳性能在同时使用可学习乘数与调优学习率时达成。性能增益在不同优化器（Adam、Muon）上均持续存在，证实其泛化能力。
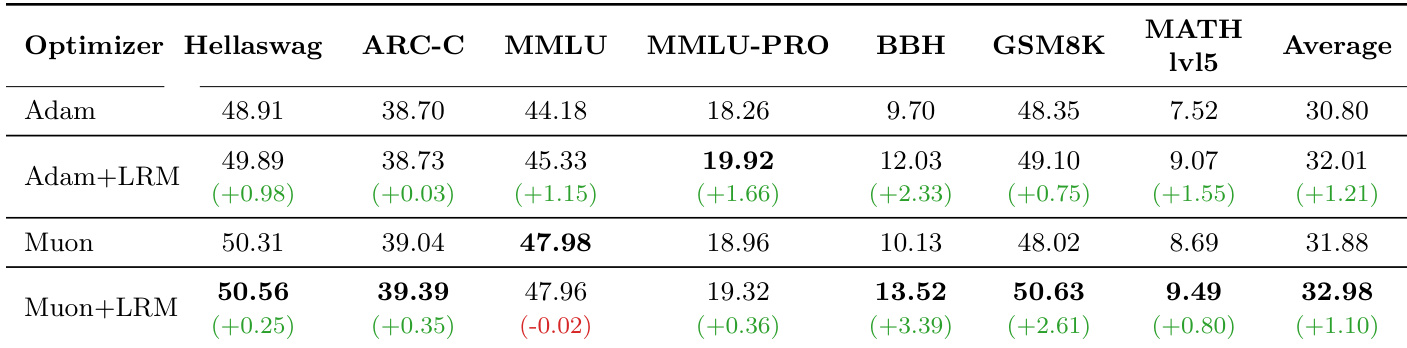
• 长周期训练验证（200GT）确认可学习乘数带来持续性能提升：Adam 下 +1.21%，Muon 下 +1.10%，在推理类基准（BBH、MATH、GSM8K）上的提升大于知识类基准（ARC-C、MMLU），表明其对模型能力的影响存在差异。

作者使用表格比较了不同优化器和基准下含与不含可学习乘数的模型性能。结果表明，添加可学习乘数能持续提升性能，其中 Muon+LRM 配置达到最高平均得分 32.98%，优于 Adam 和 Muon 基线。增益在推理任务（如 BBH、MATH、GSM8K）上最为显著，而知识类基准提升较温和。

作者使用表格比较了模型宽度的缩放方案，结果表明仅乘数方法能在不同宽度下保持恒定的激活和更新范数。结果表明，可学习乘数通过按 $d^{-1}$d−1 调整其值，实现了稳定缩放，而仅依赖学习率的常规缩放则导致激活发散和更新强度消失。