13 小时前

摘要

训练不稳定性仍是大规模语言模型（LLM）预训练中的关键挑战，常表现为突发的梯度爆炸，导致大量计算资源的浪费。本文研究了通过μP方法扩展的500万参数NanoGPT模型在训练过程中的失败现象，识别出崩溃前的两个关键先兆：（1）权重矩阵稳定秩（即Frobenius范数平方与谱范数平方之比）的快速下降；（2）相邻层雅可比矩阵之间对齐程度的持续增强。我们从理论上证明，上述两种现象共同作用会导致梯度范数随网络深度呈指数级增长。为打破这一不稳定性机制，我们提出一种新型优化器MSign，该方法周期性地对权重矩阵施加矩阵符号（matrix sign）操作，以恢复其稳定秩。在参数规模从500万到30亿的多个模型上进行的实验表明，MSign能够有效防止训练失败，且计算开销低于7.0%。

一句话总结

清华大学与微软的研究人员提出了 MSign 优化器，该优化器通过矩阵符号运算恢复权重矩阵的稳定秩，从而稳定大语言模型训练，可防止从 5M 到 3B 参数规模模型的梯度爆炸，计算开销低于 7%。

主要贡献

我们识别出稳定秩坍塌和相邻层雅可比矩阵对齐度增加是大语言模型训练失败的关键前兆，并证明二者结合会引发随网络深度指数增长的梯度。
我们提出 MSign 优化器，该优化器周期性地应用矩阵符号运算以恢复稳定秩，从而打破不稳定性机制，同时不影响训练动态。
在 5M 至 3B 参数规模的模型上实验表明，MSign 可在低于 7.0% 的计算开销下防止梯度爆炸，验证其在密集模型和 MoE 架构上的有效性。

引言

作者利用矩阵分析与雅可比动态的洞见，解决大语言模型训练中的不稳定性问题——这一关键问题常因不可预测的梯度爆炸而浪费大量计算资源。以往工作常将不稳定性视为症状，采用裁剪或调度等方法，而未针对根本原因：权重矩阵稳定秩坍塌与相邻层雅可比矩阵对齐度增加，二者共同触发梯度指数增长。本文主要贡献为 MSign 优化器，该优化器周期性应用矩阵符号运算恢复稳定秩，从而打破不稳定性反馈循环。在 5M 至 3B 参数规模的模型上验证，MSign 以低于 7% 的开销防止训练失败，且仅需干预注意力投影层。

顶部图示

方法

作者利用理论框架解释 Transformer 模型训练不稳定性，核心在于稳定秩坍塌与雅可比对齐的相互作用。分析从标准的仅解码器 Transformer 架构开始，该架构包含 $L$ 个堆叠块，每块含多头自注意力与位置级 MLP 子层，辅以残差连接和 LayerNorm。隐藏状态 $\mathbf{H}^{(\ell-1)} \in \mathbb{R}^{T \times d}$ 通过线性投影 $\mathbf{W}_Q^{(\ell)}, \mathbf{W}_K^{(\ell)}, \mathbf{W}_V^{(\ell)}, \mathbf{W}_O^{(\ell)}$ （注意力）和 $\mathbf{W}_1^{(\ell)}, \mathbf{W}_2^{(\ell)}$ （MLP）变换。层变换记为 $\mathbf{H}^{(\ell)} = F^{(\ell)}(\mathbf{H}^{(\ell-1)})$ ，层雅可比矩阵定义为 $\mathbf{J}^{(\ell)} = \frac{\partial \operatorname{vec}(\mathbf{H}^{(\ell)})}{\partial \operatorname{vec}(\mathbf{H}^{(\ell-1)})}$ 。

核心失败机制被形式化为因果链：低稳定秩与高雅可比对齐导致总雅可比范数指数增长，进而引发大权重梯度与训练不稳定。矩阵 $\mathbf{W}$ 的稳定秩定义为 $\operatorname{srank}(\mathbf{W}) = \frac{\|\mathbf{W}\|_F^2}{\|\mathbf{W}\|_2^2}$ ，用于量化奇异值间能量分布的均匀性。对于线性层，定理 4.4 表明，在 Frobenius 范数固定时，算子范数 $\|\mathbf{W}\|_2$ 与稳定秩的平方根成反比： $\|\mathbf{W}\|_2 = \frac{\|\mathbf{W}\|_F}{\sqrt{\operatorname{srank}(\mathbf{W})}}$ 。此关系扩展至注意力与 MLP 层：注意力层雅可比范数受 $\|\mathbf{W}_V\|_2 \|\mathbf{W}_O\|_2$ 项约束，MLP 层受 $\frac{L_\phi \|\mathbf{W}_1\|_F \|\mathbf{W}_2\|_F}{\sqrt{\operatorname{srank}(\mathbf{W}_1) \cdot \operatorname{srank}(\mathbf{W}_2)}}$ 约束，其中 $L_\phi$ 为激活函数的 Lipschitz 常数。因此，所有层类型中，低稳定秩均放大层雅可比范数。

雅可比对齐定义为 $\mathbf{J}^{(\ell)}$ 的最大右奇异向量与 $\mathbf{J}^{(\ell+1)}$ 的最大左奇异向量之间的余弦相似度，可抑制矩阵乘积中的抵消效应。定理 4.2 给出总雅可比范数的下界：若每个 $\|\mathbf{J}^{(\ell)}\|_2 \geq M$ 且对齐度 $\geq a > 0$ ，则 $\|\mathbf{J}_{total}\|_2 \geq \frac{(aM)^L}{a}$ 。当 $aM > 1$ 时，该下界随深度 $L$ 指数增长，解释了观察到的梯度爆炸现象。该条件在失败阶段经验性满足，此时稳定秩坍塌推高 $M$ ，对齐度 $a$ 增加。

链的最终环节连接总雅可比范数与权重梯度大小。定理 4.8 表明，在梯度对齐假设下（包括局部梯度与雅可比奇异方向对齐），第 $i$ 层权重梯度范数下界为 $a \gamma (aM)^{L-i} \cdot \left\| \frac{\partial L}{\partial \mathbf{h}^{(L)}} \right\|_2$ ，其中 $\gamma$ 为局部梯度范数的统一下界。对所有层求和，定理 4.9 给出总梯度范数下界 $\frac{(aM)^{2L} - 1}{(aM)^2 - 1}$ ，当 $aM > 1$ 时仍随深度指数增长。

为打破此反馈循环，作者提出 MSign 优化器。该优化器周期性应用矩阵符号运算——通过 SVD 定义为 $\mathrm{sign}(\mathbf{W}) = \mathbf{U}\mathbf{V}^T$ ——以恢复稳定秩，即将所有非零奇异值设为 1。为保持尺度，结果按原始 Frobenius 范数重新缩放： $\mathbf{W}_{\mathrm{new}} = \frac{\|\mathbf{W}\|_F}{\|\mathrm{sign}(\mathbf{W})\|_F} \mathrm{sign}(\mathbf{W})$ 。实践中，MSign 每 $P$ 步（如 $P=100$ ）应用一次，可针对特定层（如注意力投影层）或所有 2D 参数，以降低计算成本同时保持效果。该干预可防止稳定秩坍塌，稳定不同规模模型的训练，经实验验证有效。

实验

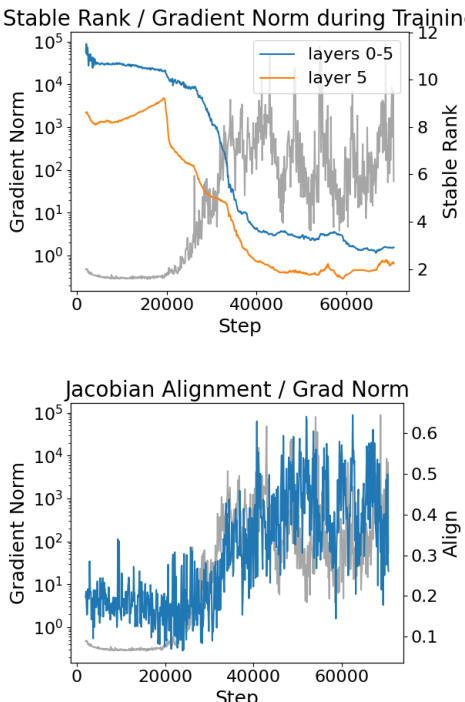
在中等学习率下，Transformer 训练失败前总出现两个一致现象：权重稳定秩急剧下降及相邻层雅可比对齐度增加，二者均与梯度爆炸相关。
MSign 能有效防止不同规模与架构（包括 MoE）模型的训练崩溃，维持梯度范数有界及损失轨迹稳定。
MSign 的理论计算开销极低（<0.1%），但实际开销较高（4–7%），因分布式 SVD 通信与核融合中断所致，但相比失败导致的浪费仍属适度。
消融研究确认 MSign 必须针对注意力层才能防止崩溃；应用于所有 2D 参数可进一步提升最终模型质量。
MSign 在 10 至 10,000 步的应用周期内均有效，但周期 ≥1000 步会引入不稳定性；推荐 P=100 以实现最佳稳定性与可接受开销。

作者使用 MSign 稳定多规模 Transformer 训练，防止梯度爆炸与损失发散，同时保持吞吐量。尽管理论开销可忽略，实测开销为 4.6% 至 6.7%，源于分布式 SVD 同步与核融合中断等实现瓶颈。结果表明，无论模型规模或架构，MSign 均能一致防止训练崩溃，且注意力层对其有效性至关重要。

作者通过周期性约束权重矩阵使用 MSign 稳定 Transformer 训练，防止梯度爆炸与训练崩溃，无需架构更改。结果表明，仅对注意力层应用 MSign 即可维持稳定性，加入 MLP 层可进一步提升最终模型质量，即使应用于所有 2D 参数，计算开销仍适度。

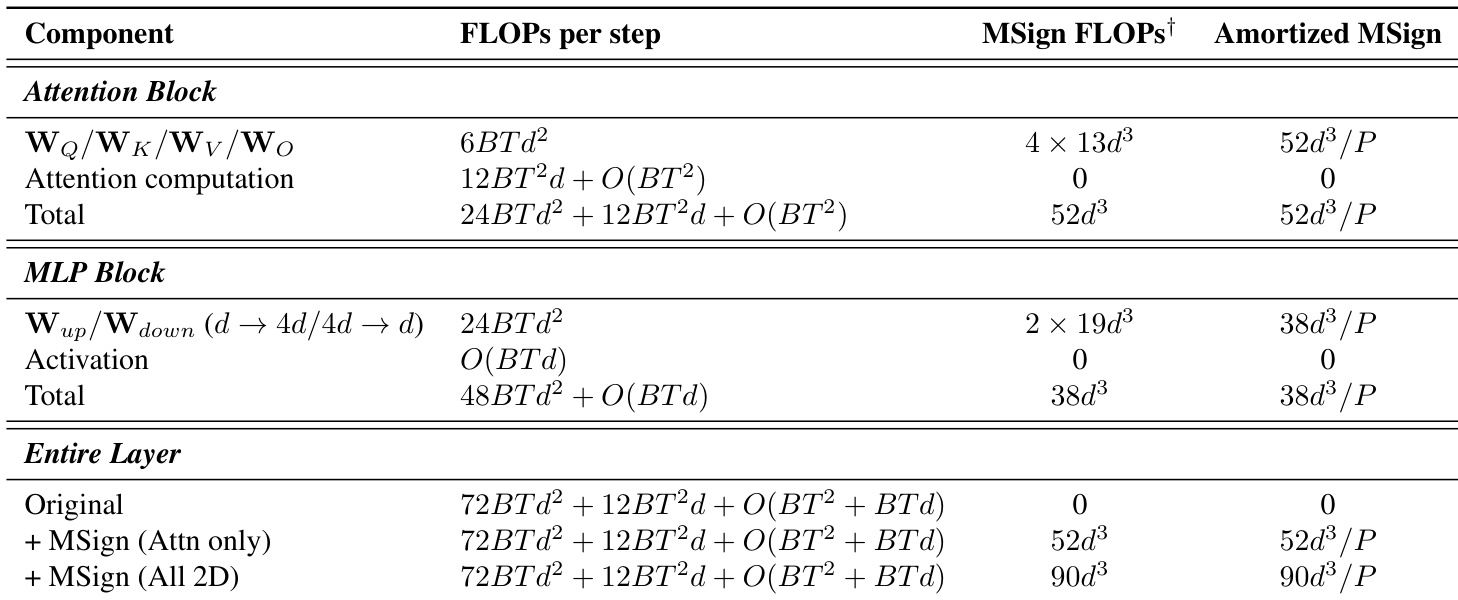
作者通过周期性控制权重矩阵属性使用 MSign 稳定 Transformer 训练，发现 10 至 10,000 步的应用周期均可防止崩溃，但更长间隔会引入瞬时不稳定性。结果表明，基于 FLOPs 的吞吐量预测乐观，实际开销源于通信与核融合中断，但相比失败成本仍属适度。推荐 P=100 以平衡稳定性与效率，维持跨模型规模的低梯度范数与平滑损失轨迹。

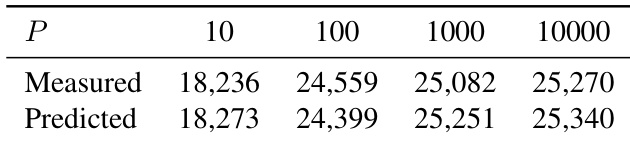
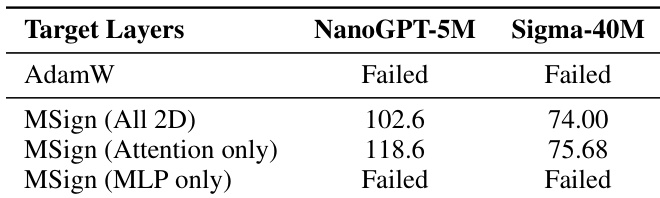
作者通过针对特定层使用 MSign 稳定 Transformer 训练，发现仅对注意力层应用可防止崩溃，而仅对 MLP 层应用则失败。结果表明，对所有 2D 参数应用 MSign 可获得最佳最终模型质量，确认注意力层是不稳定性的主要来源。

作者评估 MSign 在不同应用周期下的有效性，发现训练在周期达 10,000 步时仍稳定，但更长间隔会导致失败，表明干预频率存在关键阈值。结果表明，较短周期如 P=100 在模型质量与吞吐量间取得最佳平衡，P=10000 已出现不稳定迹象，尽管最终收敛。吞吐量在测试周期内相对稳定，但超过 P=10,000 后崩溃风险急剧上升，凸显及时干预对维持训练稳定性的必要性。