Command Palette
Search for a command to run...
MIT Develops SCIGEN, a Targeted Material for Targeted Stability, Which Can Be Adapted to Any pre-trained Diffusion model.
In materials science, the quantum properties of materials (such as topological insulation, superconductivity, and magnetic order) do not exist in isolation but are directly determined by structural properties such as the symmetry of their atomic arrangement and lattice geometry. This provides a theoretical basis for the targeted design of quantum materials through structural manipulation. However, making the leap from "theoretical possibility" to "practical usability" is not easy. Due to practical factors such as the complexity of structural manipulation and the scarcity of relevant data, progress in designing stable materials with ideal quantum properties has been slow. For example, after a decade of research, only a dozen candidate materials for quantum spin liquids have been identified.
The scientific paradigm shift driven by artificial intelligence is reshaping the methods and approaches of materials design. For example, mainstream material generation models such as CDVAE, UniMat, DiffCSP, and GNoME (mostly based on diffusion models or graph neural network architectures) have demonstrated tremendous potential in identifying stable crystal structures and batch-generating millions of candidate materials.However, most methods still rely on sampling from the statistical distribution of training data, resulting in the output materials being limited to common types in existing databases in terms of structural topology and performance characteristics.However, crystallographic space groups only provide a macroscopic structural framework for a material, failing to capture the crucial local geometric patterns. Therefore, developing machine learning methods that can precisely embed the constraints of specific geometric patterns is key to breaking through the bottleneck of known materials and exploring new quantum phenomena.
Observe the difficulties in the research and development of quantum materials,Professor Mingda Li's team at MIT, in collaboration with Michigan State University, Oak Ridge National Laboratory, and others, proposed a geometric structural constraint integration method called SCIGEN (Structural Constraint Integration in a GENerative model).This method can be adapted to any pre-trained generative diffusion model to incorporate symmetry and geometric pattern constraints, thereby generating target materials with specific constraints. A key advantage of this method is that it eliminates the need to retrain or fine-tune the underlying model, significantly increasing the flexibility and versatility of the framework and enabling rapid adaptation to different pre-trained diffusion models, improving efficiency and speed.
The related research was published in the top journal Nature Materials under the title "Structural constraint integration in a generative model for the discovery of quantum materials."
Research highlights:
* The study proposes a solution to adapt any pre-trained diffusion generative model without retraining or fine-tuning the base model, breaking the traditional constraint generative model's reliance on secondary training of the base model.
* The method proposed by the institute has promoted the paradigm shift of quantum material discovery from "trial and error" to "directed generation", accelerating the development of quantum materials.
* The study synthesized and characterized two predicted materials, TiPd₀.₂₂Bi₀.₈₈ and Ti₀.₅Pd₁.₅Sb, which exhibit paramagnetism and diamagnetism, respectively

Paper address:
https://www.nature.com/articles/s41563-025-02355-y
Follow the official account and reply to "SCIGEN Get the full PDF
More AI frontier papers:
Data support: Construction and screening of a large-scale Archimedean lattice material database
In this study, researchers used SCIGEN to compile a comprehensive database of AL (Archimedean lattices) materials for experimental exploration.
The dataset contains a total of 10.06 million materials with ALs.After a four-stage stability pre-screening, the researchers retained over 1.01 million materials. They then performed high-throughput DFT (Density Functional Theory) structural relaxation calculations on 26,000 high-priority materials, successfully converging 24,743 materials. Over 951 TP3T structures converged, and over 531 TP3T materials reached energy minima within 150 steps of structural optimization.
To identify the magnetic structure, the researchers then used a graph neural network-based classification model to identify it, where the DFT-optimized structure of 41% was identified as magnetic.
Finally, after the screening of the material data,The researchers also synthesized two new materials: TiPd₀.₂₂Bi₀.₈₈ and Ti₀.₅Pd₁.₅Sb.
Model analysis: perfect design logic and improve material generation model capabilities
SCIGEN integrates geometric constraints directly into the diffusion generation process, enabling material generation models to more efficiently explore stable quantum materials with target geometry and quantum properties. Using a "constraint guidance-mask iteration-denoising convergence" logic chain, starting from the target constraint, random constrained structures are diffused over multiple time steps. Before each diffusion, the constrained structure masks the denoised structure, forming an inductive bias that guides the generation process toward producing output that meets the constraints. By iteratively applying masking in each denoising step, all atoms belonging to the mask are deterministically converged to positions across all imposed geometric structures. Therefore, SCIGEN ensures that the generated materials meet the preset geometric constraints while retaining the generative validity of the underlying model.
Specifically, the goal of crystal structure generation is to find a periodic crystal M, which can be composed of three components,These are: a lattice matrix L = [l₁, l₂, l₃] ∈ R³ᕽ³, containing three basis vectors, describing the overall spatial framework of the crystal; fractional coordinates F = [f₁, f₂, …, f៷] ∈ [0, 1)³ᕽᴺ, representing the relative positions of atoms in the lattice (limited to the range [0, 1) to reflect periodicity); and a one-hot atom type encoding A = [a₁, a₂, …, a៷] ∈ [0, 1)ʰᕽᴺ, which uses a binary code to identify the specific type of each atom. During diffusion-based material generation, SCIGEN applies geometric constraints to L, F, and A to ensure that the generated structure conforms to the target morphology.
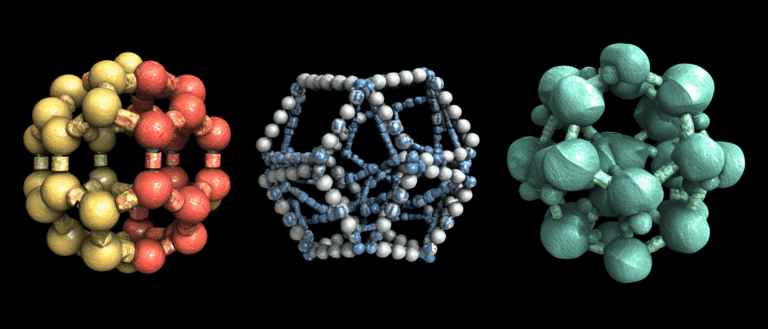
As shown in Figure a below,Representative lattices that SCIGEN can constrain include triangular lattices, honeycomb lattices, and Kagome lattices.These are the core structures that host unique quantum phenomena such as quantum spin liquids.
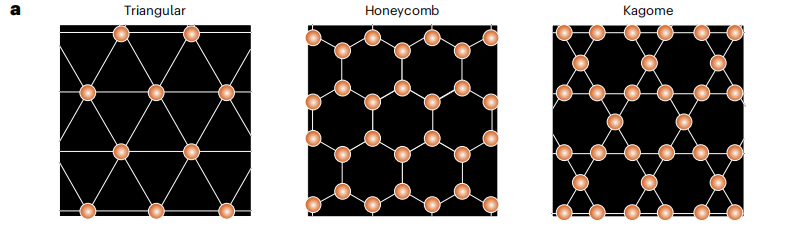
Figure b below illustrates the constrained structure initialization process. The core rules for initializing constrained structures are based on an "Archimedean lattice composed of magnetic atoms," ensuring that the constrained structure possesses potential quantum properties from the outset. Figure c illustrates the generation algorithm for integrated constraint components, visually presenting the complete process of "constrained structure diffusion - unconstrained structure initialization - fusion of the two - iterative denoising."
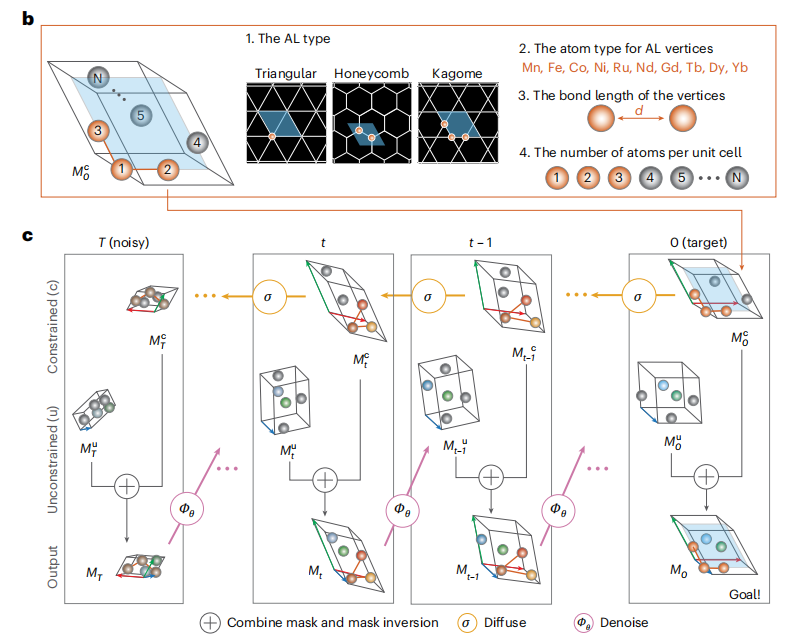
Among them, the core of SCIGEN from initialization to generating the final structure M₀ is the "iterative integration of constrained and unconstrained components."First, the initialized constraint structure (such as AL composed of magnetic atoms) is subjected to noise addition for T=1000 steps to obtain the constraint structure Mᶜₜ (t∈[1, T]) at each time step.This step provides a "pre-set path" for denoising the constrained components, preventing subsequent generation from deviating from the target geometry. The unconstrained structure initially consists of a completely noisy Mᵘₜ, representing the portion of the generation process that can be freely optimized. These two structures are then integrated to form the composite structure MT, which is then denoised to yield Mᵘₜ₋₁. This logic is repeated in all subsequent steps, ultimately guiding some atoms to form the AL planar structure through iteration, resulting in the target crystal structure M₀.
To prove the effectiveness of SCIGEN constraints,The study also proved from both mathematical proof and computational verification that SCIGEN does not destroy the original distribution of the underlying model when imposing constraints.After generating a large number of materials, the stability is evaluated through "four-stage pre-screening + high-throughput DFT relaxation" to ensure that potentially stable quantum material candidates are screened out.
* A four-stage pre-screening process combines chemical rules that check charge neutrality and the volume of the unit cell occupied by atoms with an auxiliary neural network that predicts stability based on the convex hull energy Eₕᵤₗₗ value (the lower the Eₕᵤₗₗ value, the more thermodynamically stable the material).
* High-throughput DFT relaxation performs density functional theory calculations on the screened materials. Through structural relaxation (optimizing atomic positions and unit cell dimensions), we ultimately identify candidates with potential stability, providing a basis for subsequent experimental synthesis or in-depth research.
Experimental verification: SCIGEN demonstrates outstanding directional generation and material prediction capabilities
In the specific experiment, the basic model adopted the DiffCSP model, which also verified the retention of the basic generation model capabilities.
first,The experiments show the results of material generation under three main AL constraints:The directional generation capability of SCIGEN is verified based on the triangular lattice, honeycomb lattice, and Kagome lattice, as shown in the figure below.
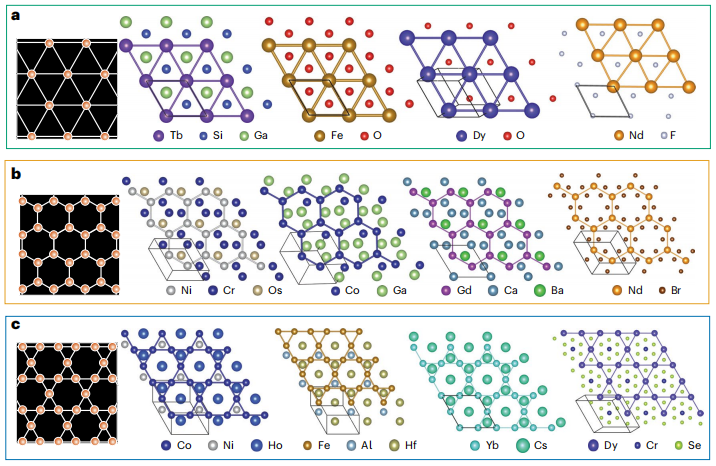
The results show thatSCIGEN can precisely guide constrained atoms to arrange into predefined geometric patterns, and the constraints only act on the target components.The positions of unconstrained atoms are not strictly defined, ensuring a directed and flexible generation process. The positions of unconstrained atoms are naturally determined during the generation process, influenced by spatial and bonding factors. For triangular lattices, unconstrained atoms tend to occupy positions connecting three magnetic atoms, forming equilateral triangles. For honeycomb lattices, unconstrained atoms typically appear at the center of hexagons formed by magnetic atoms, coplanar with the lattice planes. For Kagome lattices, unconstrained atoms connect the equilateral triangles and hexagons of each Kagome lattice layer. If the internal space of the lattice polygon is too narrow, they will be offset outside the AL plane. For larger polygons, such as hexagons, they can be arranged coplanar with the constrained atoms.
To generate confined material structures with a higher likelihood of stability, the researchers also designed an initial condition sampling scheme by analyzing pre-screening survival rates. The key is to determine the optimal choice of "number of atoms per unit cell (N)" and "type of magnetic atoms at the AL vertices." The researchers first sampled N values from a uniform distribution and calculated the corresponding "multi-stage pre-screening survival rates" for different N values to obtain a stable probability distribution for N. Based on this distribution, N was then sampled to initialize large-scale generation: triangular lattices are more suitable for smaller N values, while honeycomb and Kagome lattices are more suitable for larger N values. This is shown in Figure d below.
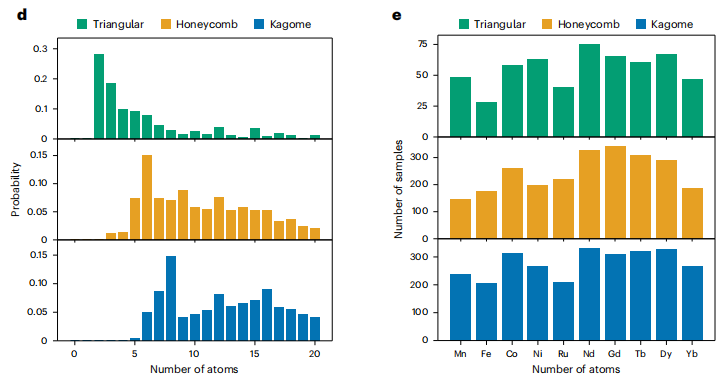
Figure e: The amount of material remaining after pre-screening for common magnetic atom types in each major geometric pattern.
As shown in Figure e above, 10 common magnetic atoms (Mn, Fe, Co, Ni, Ru, Nd, Gd, Tb, Dy, Yb) were tested experimentally.3,000 materials were generated for each lattice type and each magnetic atom, and the number of stable materials after pre-screening was counted.The results show that although the amount of stable materials varies for different magnetic atoms, all 10 types of magnetic atoms can form AL structures. Therefore, when generating them on a large scale, "equal probability sampling" is used for the AL vertex atom types to take into account both diversity and stability.
In addition to the three main lattices mentioned above, SCIGEN can also be applied to other Archimedean lattices, such as squares, elongated triangles, and truncated squares, totaling seven types of AL-constrained materials. Unconstrained atoms also play a key role in these lattices, bridging the gaps between lattice layers, enhancing the mechanical and thermal stability of the structure. They can even spontaneously form recognizable AL patterns, suggesting that AL structures have a "fixed stability preference" in local coordinates, providing a foundation for the exploration of more unique quantum materials. (See the figure below.)

As a variation of the square AL,The researchers also experimentally demonstrated SCIGEN's breakthrough in generating Lieb lattice materials.Results show that SCIGEN can generate stable Lieb-like lattice materials through geometric constraints, validating its ability to generate scarce lattice structures. In these Lieb-like materials, magnetic atoms such as Tb and Dy are oriented at the nodes of the Lieb lattice, laying the foundation for magnetic property studies. Subsequent DFT structural relaxation calculations on the generated materials revealed that the overall Lieb lattice architecture remains intact. Further band calculations revealed that these materials exhibit the expected electronic flat band characteristics near the Fermi level, confirming that the SCIGEN-generated materials are not only structurally stable but also exhibit the unique quantum electronic behavior of the Lieb lattice. This is shown in the figure below.
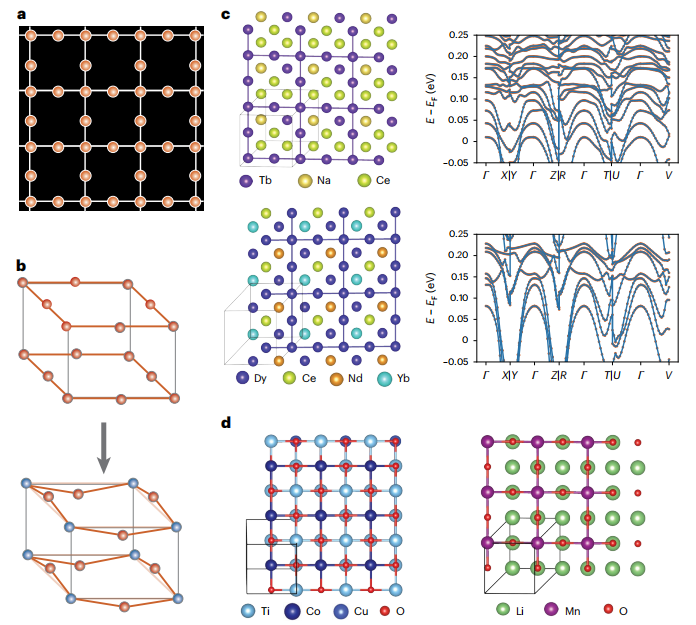
To push Lieb-like lattice materials toward oxide analogs of practical superconducting materials, SCIGEN introduced an "adaptive demasking" strategy that balances constraint rigidity and structural flexibility, building a bridge between basic research on Lieb lattices and exploration of superconducting applications.
To verify the predictive ability and effectiveness of SCIGEN,The researchers synthesized and tested two completely new compounds – TiPd₀.₂₂Bi₀.₈₈ and Ti₀.₅Pd₁.₅Sb.Experiments show that although they have slight differences in stoichiometry and crystal symmetry from their counterparts predicted by SCIGEN, the experimental results are still highly consistent with the calculated results. The former exhibits paramagnetism and the latter exhibits diamagnetism.This demonstrates the ability of SCIGEN to propose chemically plausible structural motifs, which, although not in idealized form, can still provide a basis and value for further exploration.
In summary, SCIGEN, as an innovative general machine learning-based framework, opens up previously inaccessible areas in the materials design space, paving the way for breakthroughs in quantum materials based on the relationship between structure and performance.
Quantum material discovery and artificial intelligence collide to create brilliant fireworks
The "structure-performance relationship" has become a core concept in the current research and development of new materials. It has two key benefits: first, understanding the functional quantum phenomena of materials through structure; second, predicting the material's microstructure through performance, and then, through structure manipulation, enabling targeted design of target materials. The development of artificial intelligence is undoubtedly paving a new "highway" for scientists to systematically study the relationship between these two aspects, providing new opportunities for accelerating the research and development of new materials.
In addition to the above achievements, the scientific research community has a long history of studying the structure-performance relationship, such as the research on the basic model mentioned in the article.Among them, the Google DeepMind team published a study titled "Scaling deep learning for materials discovery".A method called GNoME (graph networks for materials exploration) is proposed to achieve machine learning extension of materials exploration through large-scale active learning.
The method is based on two key components: first, establishing methods for generating diverse candidate structures, such as symmetry-aware partial substitution (SAPS) and random structure search; and second, using advanced graph neural networks (GNNs) to predict the total crystal energy. In an iterative process, the GNoME model uses existing data to train and screen candidate structures. DFT energy calculations verify the predictions and provide data for the next round of training. Ultimately, over 2.2 million stable structures were discovered.The updated convex hull contains 381,000 new entries.The number of stable crystals has been expanded by an order of magnitude compared to before.
Paper address:
https://www.nature.com/articles/s41586-023-06735-9
The underlying model used in the aforementioned experiments comes from a study titled "Crystal Structure Prediction by Joint Equivariant Diffusion," conducted by teams from Tsinghua University, Renmin University of China, and Sun Yat-sen University.The study proposed a method called DiffCSP to solve the difficult problem of crystal structure prediction.The model is designed based on a periodic equivariant denoising model and jointly generates the lattice and atomic coordinates of each crystal, which can better model the crystal geometry.
Paper address:
https://arxiv.org/abs/2309.04475
In summary, the SCIGEN method is an innovation based on prior findings. It refines the basic diffusion model through "constrained integration," opens up a new, targeted and efficient path for the discovery of quantum materials, and promotes quantum material research and development from "scaled trial and error" to "directed design." Its versatility also lays the core framework foundation for the subsequent exploration of materials with unknown quantum structures and properties.